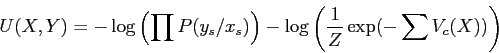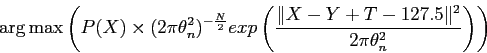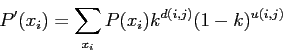Binarisation
Champs de Markov
Du fait de la forte variabilité inhérente aux documents, une modélisation formelle de la structure est difficilement envisageable, car trop rigide. Les modèles stochastiques s'accommodent mieux des incertitudes. Les champs de Markov permettant de représenter une relation de voisinage, ils sont particulièrement adaptés à la segmentation puisqu'il existe beaucoup de relations spatiales dans une image. La théorie des champs Markoviens a donc été largement développée ces dernières décennies et appliquée dans différents domaines du traitement d'image \cite{Li95}. La segmentation (et \textsl{a fortiori} la binarisation) se ramenant à la définition de la classe
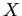
d'un pixel en fonction de sa valeur
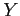
, le problème est donc de calculer la configuration optimale du champ d'étiquettes
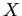
qui maximise la probabilité
a posteriori 
. Grâce au théorème de Bayes, on a
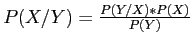
, ce qui est plus facile à caractériser. En appliquant les hypothèses Markoviennes et d'indépendance entre les observations, on obtient :
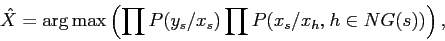 |
(10) |
avec
-

désigne le voisinage du site s ;
-

représente la vraisemblance de la classe par rapport à l'observation ;
-

représente la connaissance contextuelle introduite par le modèle.
Il s'agit de la probabilité
a priori de la configuration
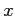
du champ
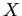
. Afin de rendre calculable cette estimation, ce terme peut être réécrit ainsi :
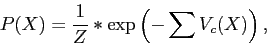 |
(11) |
avec :
-
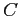
un ensemble de cliques associés au voisinage

(Une clique étant un sous-ensemble de sites mutuellement voisins) ;
-

est la fonction de potentiel de la clique
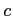
;
-
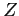
est un terme de normalisation.
On peut ainsi introduire la notion d'énergie en calculant le logarithme négatif de la probabilité jointe

, soit :
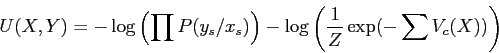 |
(12) |
 |
(13) |
Finalement le problème de la segmentation revient à un problème de minimisation de la fonction d'énergie :
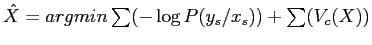
. Cette fonction d'énergie peut être minimisée en utilisant un algorithme d'optimisation, comme le recuit simulé.
Pour simplifier les calculs de binarisation, on suppose que le bruit qui vient perturber les observations suit une loi de Gauss. Ainsi,
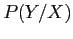
est approximé de cette manière :
 | (14) |
en prenant
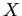
={0,255} et
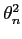
la variance. Cependant, cette estimation est trop réductrice car les valeurs de
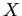
ne sont pas toujours aussi extrêmes : le texte n'est pas toujours à 0 mais peut être à 10 par exemple, à cause du bruit. L'idée de Wolf est alors d'ajouter une fonction
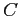
pour modifier les valeurs de
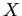
lors du calcul du bruit résiduel (

). Hélas, la fonction
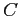
, qui revient à trouver l'incidence du bruit sur chaque pixel, n'est pas calculable simplement. Il décide alors d'utiliser le calcul de Sauvola [#!Sauvola00!#] pour adapter localement le calcul du bruit résiduel. La fonction d'énergie devient alors
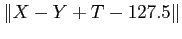
, avec
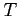
le seuil calculé avec la méthode de Sauvola. Donc le problème du maximum
a posteriori peut se calculer ainsi :
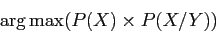 |
(15) |
, soit
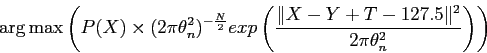 |
(16) |
La variance
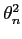
est approximée en regardant dans une fenêtre centrée autour du pixel et séparant l'histogramme en deux classes en utilisant le critère d'Otsu (qui revient à maximiser la variance intra classe) [#!Otsu79!#].
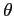
est alors calculé en multipliant par une constante (fixé à
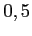
) la variation intra classe.
Enfin, le calcul de
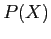
, ou plutôt d'après l'équation
2.11, le calcul de

se fait d'après la fréquence d'occurrence dans une clique de chaque classe, par apprentissage. Le calcul de

est celui ci :
 |
(17) |
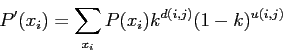 |
(18) |
où

est la probabilité de trouver la classe

dans la clique

.
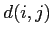
est le nombre de bits différents entre deux cliques de classes

et

.
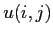
est le nombre de bits identiques entre deux cliques de classes

et

.
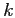
est un coefficient de lissage.
L'algorithme de Wolf constitue ainsi l'extension de la méthode de Sauvola et les résultats présentés montrent un gain important par rapport à cette méthode, ce qui justifie l'utilisation de champs de Markov.