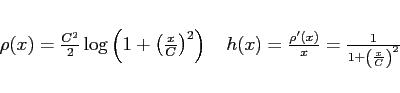Estimateurs robustes
L'algorithme de filtrage de Wiener modifié appartient en fait à une classe d'algorithmes de filtrage dite à "préservation du contour". Les approches les plus populaires sont cependant celles basées sur les estimateurs robustes. Dans le cadre de la restauration d'image, l'estimation cherche à approcher la "vraie " valeur du pixel. Le problème principal de la méthode des moindres carrés est qu'elle fournit des résultats erronés au voisinage des contours. En effet, aux contours, deux modèles de caractéristiques s'opposent de part et d'autre de la frontière et l'approximation par les moindres carrés ne résout pas correctement ce cas de figure. Un estimateur robuste est un estimateur statistique dont on cherche à minimiser l'influence de données atypiques sur l'estimation. Il existe plusieurs catégories d'estimateurs robustes.
Filtres d'ordre
Les filtres d'ordre sont une famille d'estimateurs très utilisée. On considère un voisinage autour du pixel. En supposant que l'image est stationnaire dans la fenêtre et que le bruit est additif, la valeur des pixels bruités sera loin des valeurs du centre. Le filtre s'écrit alors
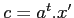 avec
avec

|

|
| (a) | (b) |
| Fig 2.3 - Exemple de filtres. (a) Image Lena avec bruit et écriture. (b) Image après filtrage par la médiane. | |
Un cas particulier de ce filtre est le filtre de la médiane, en choisissant le vecteur
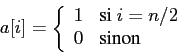
Ce filtre élimine efficacement le bruit. Il permet donc d'enlever les valeurs aberrantes, dû le plus souvent au bruit. Mais on se rend bien compte que si l'on prend une grande fenêtre, l'hypothèse de stationnarité n'est plus respectée, et l'on peut voir apparaître un phénomène d'étalement, comme avec une peinture à la gouache.
M-estimateurs
Une autre famille très utilisée est celle des M-estimateurs. C'est une généralisation de l'estimation aux moindres carrés. Le vecteur M-estimé
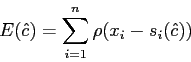 |
(3) |
-
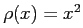 , on est ramené à l'estimateur des moindres carrés);
, on est ramené à l'estimateur des moindres carrés);
-
-
D'où :
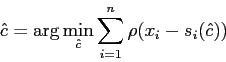 |
(4) |
F. Bouchara. Traitement d’image pour la vision,
support de cours, 2006
[Bou06].
support de cours, 2006
Dans sa mise en
L'intérêt d'un estimateur robuste est de pouvoir supprimer le bruit dit de "poivre et sel ", c'est-à-dire un bruit ponctuel mais fort. Ce bruit en image est causé notamment par les décharges électriques des capteurs.
Conclusion
Il existe d'autres solutions de restauration, comme la prise en compte de plusieurs images dans une vidéo, mais leur nombre et leur intérêt pour notre sujet rendent leur présentation peu utile. On trouvera ailleurs
M.R. Banham and A.K. Katsaggelos. Digital image restoration Signal Processing Magazine, IEEE,
14(2) :24–41, 1997
[BK97] un état de l'art conséquent sur les techniques de restauration d'images ainsi que plus de détail sur différentes techniques, comme la restauration d'images fortement compressées par JPEG.14(2) :24–41, 1997
  |  |  |