Filtrage de Wiener adaptatif

Adaptation du filtre de Wiener

Une adaptation du filtre de Wiener a été conçue pour se comporter comme un filtre passe-bas sur les zones uniformes tout en conservant les discontinuités. La modification du filtre permet de le rendre adaptatif à l'image. Le filtre peut s'exprimer ainsi :

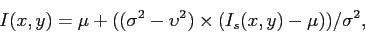$I (x, y) = \mu + ((\sigma^{2} - \upsilon^{2})\times(I_{s}(x, y) - \mu))/ \sigma^{2}$

(2)

Avec
-

: image filtrée ;
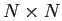- $\mu$ : moyenne des valeurs des pixels dans une fenêtre de taille $N\times N$ centrée en ( $x,y$

) ;
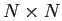- $\sigma$ : variance des valeurs des pixels dans une fenêtre de taille $N\times N$ centrée en ( $x,y$

) ;
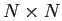- $\upsilon$ : moyenne de la variance des pixels dans une fenêtre de taille $N\times N$ centrée en ( $x,y$

) ;
- $I_{s}$ : image source.

Bien que ce filtre améliore la qualité des documents, il ne se comporte pas bien lorsque l'image est fortement bruitée. Le filtre est cependant utilisé par des technique de binarisation, dont

B. Gatos, I. Pratikakis, and S. J. Perantonis. Adaptive degraded document image binarization.Pattern Recogn.
:317–327, 2006

[GPP06] car il est tout particulièrement adapté à la restauration de documents. Il permet d'augmenter le contraste entre le texte et le fond tout en lissant le fond. De plus, il se comporte aussi bien sur des documents manuscrits que sur des documents imprimés, car aucune hypothèse n'est faite sur la forme des discontinuités.


(a)	(b)
Fig 2.2 - Exemple de filtres. (a) Image d'origine. (b) Image après filtrage de Wiener adaptatif.